「目→的」はベクトルだ！
＜三角錐を内包する象徴方程式＞

「ある」から「なる」の視点に立つ
http://www.beach.jp/circleboard/ad00178/topic/1100200088592

の続きです。

ベクトルの意味がこんなに深いとは思ってもいませんでしたが、もう一度、ベクトルとは何かを確認しておきましょう。何か錯誤しているかも知れません。

先ず、四元数Q=(t,V)のVはベクトルであり、ベクトルは「向きをもった線」だったですよね。向きと線があればベクトルなのですからベクトルそのものには世界の中のどこに「ある」という座標は不要なのですね。何かかがどこかに「ある」と思うなら世界内存在であり、世界の中のどこに「いる・ある」という位置を示す座標が必要なのですが、自分が円錐だと思って、それが世界だと思うなら、外の世界を想定する必要がないのですね。実際、私達は多くの時間をそういった有り様で生きているのですね。自分自身がMPであり、ベクトルの根っこであり、指し示す対象の先端なのですね。

いつも、いつも自分は会社のどの組織に所属しているのだろうなどとは意識などはしていないのですよね。意識するのは人事異動の季節とか外部で組織を代表して意見を述べるときとか名刺を交換するときぐらいではないでしょうか？

自分が中心になって何かをするときは、今自分がどっちを向いているのかという方向(目的)を意識していれば、大概は無意識に何でもやってしまうのですね。泥酔してもちゃんと帰ってこられるのはまさにベクトルを持っているからなのですね。いちいち世界座標を意識する必要はないのですね。それがナビに頼ってしまうと、そうはいかないのですね。

ゲームでも同様でワールドビューやローカルビューが必要になってきますが、それは見せるために必要な座標であって、回転を計算するためには必要がないのですね。

プールの話に戻りましょう。

プールの外にいるならストップウオッチを持っていれば、泳ぐ人が次にどこにいるのかは予測できますが、泳ぐ人自身はどうやってターンなどの位置が分かるのでしょうか？

盲目状態で位置が分かる方法があれば、良いのですよね。それって、コウモリですね。それではコウモリになったつもりになりましょう。「なる」のです。コウモリは超音波を使って障害物を避け上手く飛び回っているようですね。コウモリと同じ方法を使えば世界の中に「いる」自分という設定をしなくても位置を知ることができるということですね。

確かに、コウモリは目が見えないですから世界を知らないのですよね。コウモリに与えられているのは自身の位置、障害物、超音波、耳の四つだけです。これだけで、次にいるべき位置が分かってしまうのですね。どんな方法を使っているのでしょうね。

これを下の図で説明しましょう。

３次元の回転 (原点を通る任意方向の回転軸まわり)
http://www5d.biglobe.ne.jp/~noocyte/Programming/Geometry/3DRotation.html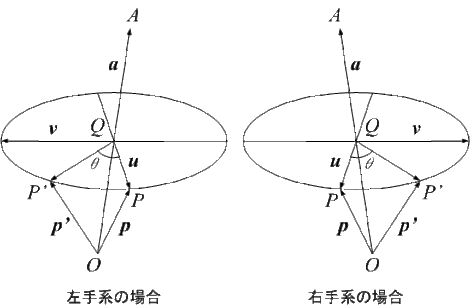

―――

円錐を耳が聞こえるコウモリとして、Pを自分の現在の位置、P'を次の位置として、Qを障害物、超音波をQPとすると反射してきた位置は分かりますね。図では角度が表現されていますが、これがポイントですね。角度が分かれば位置が分かるということが表現されているのですね。

プールの中でも同じですね。自分からプールの下に向かって超音波を発信すれは、その角度が分かれば次ぎの位置は分かりますね。角度次第なのですね。

自分が発射させた超音波と出会うためには時間が掛かりますが、それがθという角度なのですから、θは時間だということですね。時間線OAが走るのですね。もし、超音波も私も無限速度（光よりはやい）とすると、時間は０ですので、時間線は走りません。それが現在なのです。その様子が図で表現されているのですね。

ベクトルで考えるということは、時間ゼロ、無限速度で同時に考えるということのようですね。こういうのが観念的同時の認識なのでしょうかね。

図では直観的に理解できますが、実際には計算しないといけませんよね。コウモリはどんな計算をしているのでしょうね。しかし、コウモリに聞くわけにもいきませんね。ここまで分かってきたので、後はコウモリから離れてゲームの世界に入りましょう。ゲームのプログラマーはどうやってそれを計算しているのでしょうね。

常識ならコンパスで円を描いて分度器を当てれば一発ですが、それでは限界がありますね。第一描いているうちに時間が立ってしまいます。タイミングが重要なのですね。ゲームの世界ではコンピュータの中にアバタをつくりそれを動かすのですね。ですから、移動するスピードより早く計算できないと使いものにならないのですね。これはゲームに限らずに起きる問題なのですね。例えば、応答時間です。キーボードから文字を入力するときに次の文字を入力するまでの間には時間があります。コンピュータの方は早いので余裕があるのですね。

つまり、その間を利用して他のタスクを実行しているのです。ところがタスクが多くなったり、重くなってくると、たちまち入力したけど受け入れてくれないという事態になってきます。つまり、ユーザーはいらいらしてきますね。こうした制約があるので応答時間は生命線なのですね。従って、ゲームに於いても早い計算方法が求められるのです。

ゲームのプログラマーが使うのはまるで手品のような方法なのです。こんな方法が使えると言うのも四元数というベースがあるからなのですが、それは新幹線で行くか、飛行機で行くかといった比較を超えています。ワープするような方法なのですね。

では、その種明かしをしていきましょう。先ず、用意するのは視線です。視線というのはベクトルを考えるとき極めて重要な前提なのですね。どっちを向いているのかということです。よく「ベクトルを合わせて行こう」などと言いますが、これはベクトルと言う概念の正しい使い方なのですね。ベクトルは当初、物理の世界で使われましたので、心の現象に使うのはメタファの過ぎないと思われていたのですが、ベクトルの意味が｢線分＋向き｣であるということからすると、心の領域に使っても何ら異議はないのですね。ベクトルを合わせると言うのは、同じ目的を持つということなのですね。目的というのは文字通り「目→的」ですね。目が的を向いているのですから立派なベクトルなのですね。ベクトルのこういう使い方ができることになって、ベクトルの応用が劇的に広がったとも言えるのではないでしょうか？

続く