盲目の船乗りにとって目的地を示す角度（舵角）はどうして分かる？
＜四次元能版エヴァンゲリオン：PS三角錐の応用＞

航海で使われるメルカトル図法は共形変換
http://www.beach.jp/circleboard/ad00178/topic/1100200043359

の続きです。

共形変換とは「空間の一点で交わる二つの曲線のなす角度を保つ変換のこと」と定義されていますので「角度」が必要な情報のようです。地球をそのまま小さくしたのが地球儀ですが、これを船に積んでも大海原で目的地の辿り着くことはできないでしょう。確かに、地球儀は三人称の知ではあるのですが、それによっては航海のための三人称の認識を構成できないのです。地球儀には必要な情報が表現されていないのですね。

そこで登場してきたのが「メルカトル図法」です。航海に必要な情報というのは方向です。どの方向に向かえば目的地に行けるのかです。選択の自由後は360度あります。船は三次元空間にいますが上や下には行きませんから平面上の選択で良いのですね。当時には羅針盤という三人称の知がありましたので、進むべき方角は分かったのですが問題は角度（舵角）はどうして分かるかです。東西南北の四つ方向は羅針盤で分かりますから反対の方向に行く事はありませんが、角度（舵角）が大体では目的地には辿り着けないでしょう。

大海原にいて自己（の位置を）認識するというのは大変なんですよね。航路のどの辺まで進んだというのは地球儀を眺めたって全く知りようがありません。地球儀を見れば分かるように東京からサンフランシスコに行くためには自己の位置＝経度が分からなければなりません。しかし、大海原にいる船乗りは盲目のようなものなのです。ただ、北の方向が分かるだけなのです。言える事は、自分の進む方角は四つの象限のどれかは分かっているということです。東京からサンフランシスコで言えば真っ直ぐです。しかし、大海原にいる盲目の船乗りにとって真っ直ぐとはどの角度（舵角）なのでしょうか？

自己の位置＝経度は分からなくても角度（舵角）さえ分かればなんとかなりそうですね。どうすれば角度（舵角）が分かるのでしょうか？

メルカトル図法で等角航路が直線になることのわかりやすい説明
http://fujiyamao.la.coocan.jp/0mer/01.htm

下の図を引用しました。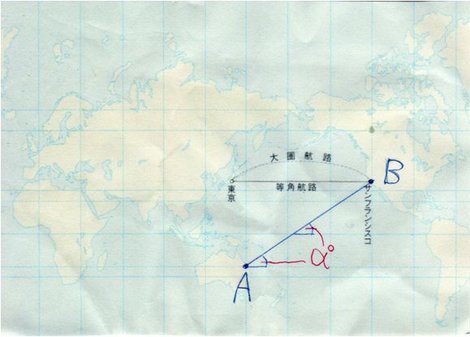

 
―――
車の運転でもでも目的地があっちの方角と言うのが分かれば勘に任せても行けますが、障害があって道が曲がったりしていので方角が分からなくなってしまうことがあります。如何に一人称の勘は当てにならないかを知ることになります。まして大航海時代は、嵐もあったりして思い通りには進めないでしょう。食料も少なくなっていきますから不安だったでしょうね。そんなときのメルカトル図法は盲目の船乗りに取ってはまさに神の目だったのではないでしょうか？

航海に必要な情報、確実に目的地に辿りつける三人称の情報とは何かということですね。それが「メルカトル図法」で表現された等角航路であり、「舵角」だということなのですね。

メルカトル図法では出発地点と目的地を結ぶ航路は直線になります。つくり方などはメ「ルカトル図法で等角航路が直線になることのわかりやすい説明」にありますので、こちらを参照してください。四次元能の関心は、これがどうして、「三人称を突然に一人称に変換して、再び三人称に構成する。」という海舌氏の共形変換なのかということですね。まだ、イメージが掴めていません。

メルカトル図法の地図は地球儀を平面化したものですので、いろいろと不都合も生まれるのですね。上の方が異常に膨らんでいたりします。それでも盲目の船乗りにとっては

三種の神器＝三人称の知（羅針盤＋メルカトル図法の地図＋等角航路

だったようですね。

こうして地球という三次元を二次元（平面＝メルカトル図法）にして三種の神器を得た船乗りは勇気百倍で実際の航海に出ます。そこで突然に一人称（船乗り）となるのですが、もはや盲目の船乗りではありません。三人称の知の助けを借りて三次元を再構成するのですね。つまり、三次元の地球という目的地に辿り着くことを成し遂げるのです。

船乗りの航海を端的に表現すれば「三人称を突然に一人称に変換して、再び三人称に構成する。」という海舌氏の共形変換を船乗りが実践したことになります。

続く